Важной частью технического задания на создание АСУП является постановка экономических задач, которые будут решаться разрабатываемой системой управления.
Назначение разработки
Для лучшего понимания поставленной перед алгоритмистом и программистом проблемы в техническом задании указывается, в каких ситуациях возникает необходимость решения данной задачи, где и кем эта задача должна решаться, как используются результаты решения и как часто она решается. В техническом задании указывается основание для данной разработки и ожидаемый экономический эффект.
Постановка задачи
Постановка задачи заключается в формулировании исходных посылок, требуемых результатов решения задачи и описании ее математического содержания. Изложение задачи должно быть корректным и освещать следующие вопросы:
- организационно-экономическую сущность задачи, которая характеризуется наименованием задачи и кругом объектов, для для которых она предназначена; экономическим обоснованием необходимости ее включения в комплекс задач, решаемых ЭВМ; шифром документа и местом хранения контрольного примера по данной задаче;
- содержание постановки задачи, которое включает формулировку условий и ограничений, учитываемых при создании математической модели; возможные критерии оптимальности для задач оптимального планирования; возможные логические разветвления в решении задачи; ограничения на область решения задачи; дополнительные сведения, включающие перечень известных публикаций, касающихся данной задачи или сходных с ней, а также опубликованные расчетные формулы и алгоритмы;
- периодичность решения задачи;
- связь данной задачи с другими и ее место в комплексе задач; при разработке комплекса задач, связанных друг с другом по логике решения или информационно, описывается схема функциональных и информационных связей между отдельными задачами комплекса, перечисляются все массивы данных, которые используются в рассматриваемой задаче или формируются в результате ее решения для других задач комплекса. Кроме того, указываются ограничения, налагаемые на данную задачу со стороны смежных задач (необходимость предварительного получения используемых результатов смежных задач, необходимость получения промежуточных результатов);
- организацию сбора исходных данных и передачи их в обработку (с указанием используемых при этом периферийных технических средств и носителей информации);
- временные ограничения на выдачу решения задачи;
- специфические особенности задачи (если таковые имеются);
- сравнение рассмотренных вариантов задачи; обоснование целесообразности предложенного варианта с приведением параметров, свидетельствующих в пользу данного варианта.
Организация информации
Постановка задачи должна сопровождаться описанием массивов исходных данных и документов, используемых в задаче и получаемых в результате ее решения. Информация, используемая при решении задачи, разделяется на условно-постоянную и условно-переменную. К условно-постоянной информации относится такая, которая содержит сведения об изделиях, оборудовании, ресурсах рабочей силы и материалов, нормативах (нормы расхода материалов, рабочего времени, расценки), константах, указывающих размерность решаемых задач. Условно-переменная информация содержит сведения о состоянии производства в некоторый конкретный момент времени и информацию, получаемую из решения других задач комплекса.
Входная условно-переменная информация. Приводятся формы входных документов (в приложении к постановке) в таком виде, в каком они будут поступать для решения задачи, либо макеты сообщений на машинных носителях информации (если первичный носитель является машинным). По каждой из форм приводятся: шифр или условное обозначение (шифр) формы документа; периодичность и ориентировочные сроки поступления; максимальное количество документострок; перфорируемые реквизиты; способ обнаружения ошибок в информации; наименование задачи или источника, из которого поступает машинный документ.
Для каждою вида документов необходимо привести макет для перфорации, если он определен, с указанием колонок для каждого реквизита в случае набивки на перфокарты; с указанием последовательности реквизитов
разделительных знаков в случае набивки на перфоленту. Описание макета (структуры) документа, поступающего с магнитной ленты, перфокарт или перфоленты, производится в точном соответствии со стандартами, принятыми в разрабатывающей организации. Все сведения рекомендуется указывать на чертеже формы документа. Кроме того, оформляется перечень документов входной переменной информации.
По каждому участвующему в задаче реквизиту в образце формы должно приводиться описание, которое следует вносить в графу этого реквизита в следующем виде: обозначение реквизита; длина реквизита в знаках; диапазон изменения; единица измерения (если не указано в шапке документа). В случае если вид документа не позволяет составить указанное описание непосредственно на бланке документа, допускается оформление описания соответствующих реквизитов по каждому документу в виде следующей таблицы
Форма описания документа
|
Порядок шифров реквизитов |
Наименование реквизита |
Условное обозначение реквизита |
Количество цифр |
Номер колонки на перфокарте |
||
|
целая часть |
дробная часть |
с |
по |
|||
|
01 |
Шифр цеха |
ЩЦ |
3 |
— |
1 |
2 |
|
02 |
Шифр изделия |
ШИ |
2 |
— |
3 |
5 |
|
03 |
Шифр единицы измерения |
ШЕИ |
2 |
— |
6 |
7 |
|
04 |
Планово-расчетная цена единицы измерения |
ПРЦ |
6 |
3 |
8 |
16 |
В случае большого количества документов переменной информации (свыше 10) рекомендуется дополнительно представлять «Сводный перечень Документов переменной информации», заполняемый в определенной форме
Сводный перечень документов переменной информации
|
Условное обозначение документа |
Наименование документа |
Количество документов в массиве (пределы изменения) |
Порядок шифров реквизитов для сортирования |
Периодичность заполнения источника образования документа |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
М-02 |
Состав сборочных соединений |
300 |
01. 02. 03. |
31 |
Входная условно-постоянная информация. Она делится на нормативную информацию (НСИ) и константы. Как правило, ПСИ представляет собой значительные по объему массивы данных, содержащихся на различного рода носителях (документах, перфокартах, перфоленте, магнитной ленте и т. п.). Входные массивы НСИ описываются следующим образом: источник массива вводится с внешних носителей информации; структура массива — «справочник» (из каких разделов состоит массив и в какой последовательности расположен массив, разбиение массива на части, заглавия частей или подразделений); структура каждого вида документа в массиве, т. е. перечень реквизитов в документе.
Формы документов, необходимые для формирования НСИ, приводятся в приложении к задаче, по каждой из форм должны быть приведены те же сведения, что и для входной переменной информации. Указываются необходимые сведения о системе шифровки реквизитов НСИ (в той части, которая содержательно используется в алгоритме решений данной задачи). Делается указание на необходимость использования готовых массивов НСИ (сформированных в уже решаемых задачах). Описание реквизитов НСИ производится аналогично описанию реквизитов документов входной переменной информации. Указываются сроки хранения НСИ (только для информации, регулярно подвергаемой полному изменению). Делается указание на необходимость резервирования добавочных реквизитов НСИ (если это требуется для подключения следующих задач).
Выходная (результативная) информация. В техническом задании должны быть даны указания, в каком виде необходимо получить результаты расчетов разрабатываются: а) формы выходных документов (либо макеты выходных сообщений на машинных носителях информации); б) формы промежуточных документов, которые должны выдаваться на печать для проверки правильности расчетов на стадии внедрения.
Все указанные формы приводятся в приложении к задаче. Каждая из выходных форм содержит сведения:
- периодичность выдачи;
- указание на обязательность (необязательность) выдачи;
- количество экземпляров;
- среднее количество строк в документе;
- требования к последовательности и сроку выдачи на ЭВМ;
- требования по упорядоченности строк (например, по возрастанию номеров или шифров некоторых объектов, по возрастанию или убыванию значения определенного реквизита и др.).
Все сведения рекомендуется указывать на чертеже формы или макета машинного документа. Описание реквизитов выходной информации производится в форме, указанной для входной переменной информации.
Формулируются специальные требования к оформлению выходных документов (например, необходимость разбиения документа на страницы и качество строк на странице при выдаче на АЦПУ, подпись должностного лица необходимость выделения отдельных строк и др.). Делается указание, по каким реквизитам-признакам и в каком порядке должен быть рассортирован массив (для вывода на АЦПУ); кроме того, необходимо указать, по изменению каких реквизитов-признаков нужно подводить промежуточные итоги. Если результаты счета должны быть выданы на АЦПУ в виде форм (табуляграмм), то должна быть расписана выходная форма на специальном бланке шириной в 128 позиции. На бланке указываются заголовок и шапка выходной формы. Кроме того, должна быть описана структура каждого вида строк, описаны все реквизиты: количество знаков, положение запятой и т. д. (табл. 9.3).
Информация, хранимая для связи с другими задачами. Материал оформляется в виде условных документов, для каждого из которых указывается: шифр или условное обозначение формы документа; максимальное количество документострок; способ обнаружения ошибок в информации; наименование задачи, из которой поступает документ.
Описание реквизитов производится так же, как и для входной переменной информации.
Информация, накапливаемая для последующих решений данной задачи, оформляется аналогично информации, хранимой для связи с другими задачами.
Информация по внесению изменений. Дается описание системы внесения изменений. Разрабатывается перечень информации, подвергающейся изменениям, и разновидностей внесения изменения. Разрабатываются формы документов (приводятся они в приложении к задаче), содержащих информацию по внесению изменений. По каждой из форм в тексте должны быть указаны: примерная периодичность поступления; периодичность внесения изменений; среднее и максимальное количество документострок при каждом внесении изменения.
Алгоритм решения задачи
На все задачи, предусмотренные для реализации в АСУП, должны быть составлены алгоритмы счета и разработана технология сбора, формирования, передачи и обработки информации. Алгоритм оформляется в виде блок-схем с необходимыми пояснениями.
Принципиальная блок-схема алгоритма должна отражать этапность алгоритмического процесса. Этапность изображается в виде блоков (совокупность процедур решения задач) с указанием взаимной связи. Внутри каждого блока кратко описывается содержание соответствующего этапа алгоритма с использованием принятых в данной задаче условных обозначений реквизитов. Символы (условные обозначения) реквизитов применяются с индексом массива цифровая часть шифра массива), из которого берется значение реквизита. Блоки нумеруются арабскими цифрами над правым верхним углом.
В принципиальной блок-схеме указываются порядок и последователь- выбора входной информации, порядок выполнения расчетов и правила для этих расчетов необходимой информации, порядок формирования промежуточных массивов и табуляграмм, порядок и последовательность вывода выходной промежуточной информации на печать и внешнюю память ЭВМ.
Пример описания структуры строк выходной формы
|
Номер реквизита |
Название реквизита |
Условное обозначение |
Количество цифр |
Ячейки буферного накопителя |
Примечание |
|||
|
делая часть |
дробная часть |
с |
по |
раз делитель |
||||
|
1 |
Шифр изделия |
ШИ |
3 |
- |
27 |
31 |
- |
|
|
2 |
Шифр единицы измерения |
ШЕИ |
2 |
- |
37 |
40 |
- |
|
|
3 |
На год |
НГ |
6 |
- |
44 |
71 |
- |
|
|
4 |
I квартал |
KBI |
6 |
- |
55 |
62 73 |
- |
|
|
5 |
II квартал |
KBII |
6 |
- |
66 |
- |
||
|
6 |
III квартал |
KBIII |
6 |
- |
77 |
104 |
- |
|
|
7 |
IV квартал |
KBIV |
6 |
- |
110 |
215 |
- |
|
|
8 |
Материалы |
М |
4 |
2 |
121 |
127 |
125 |
|
|
9 |
Покупные комплектующие изделия |
ПКИ |
5 |
2 |
233 |
142 |
140 |
|
|
10 |
Шифр изделия |
ШИ |
3 |
- |
27 |
31 |
- |
|
В принципиальной блок-схеме, как правило, не приводятся допустимый объем информации (части массива) при вводе, размещение информации в памяти ЭВМ (адреса, конкретные позиции, секторы и т. п.), элементарные циклы, т. е. детализация расчетов до уровня команд и подготовка позиций для их выполнения (переадресование, восстановление и т. п.).
Для сложных задач возможна разработка нескольких блок-схем, различных по своему уровню детализации.
Кроме предоставления принципиальной блок-схемы, в изложении алгоритма задачи дается описание развернутой блок-схемы с пояснением определенных блоков, смысл которых недостаточно ясен ил принципиальной блок-схемы или требуется дополнительная детализация и конкретизация. Поясняются отдельные выражения, применяемые в принципиальной блок-схеме Проводятся необходимые рассуждения по контролю вычислений и исправлению ошибок. В алгоритме должны быть учтены возможные варианты отклонения от нормального процесса решения задачи (например, в случае отсутствия того или иного массива информации).
Определяются требуемая точность вычисления выходных результатов, ограничения на время решения задачи, логический контроль для проверки поступающей, промежуточной и выходной информации, ограничения на длин) программ.
Проводится описание последовательных этапов счета и расчетных формул, необходимых для решения данной задачи. Разрабатываются расчетные формулы, служащие для формирования нормативно-справочной информации, а также используемые при внесении тех или иных изменений (для ссылок все формулы должны быть пронумерованы). В формулах используются обозначения реквизитов, введенных при описании документов (реквизитов).
Вычисляются соотношения в виде равенств, которые могут использоваться для контроля вычислений. Даются указания на необходимость выполнения отдельных частей алгоритма в зависимости от соблюдения тех или иных условий.
Приводятся алгоритмы либо ссылки на определенные части общего алгоритма, применяемые для различных вариантов отклонений от нормального процесса решения задачи (например, в случае отсутствия тех или иных документов, при неполной информации в отдельных документах и т. д.).
На заключительном этапе проектирования задачи осуществляются: уточнение задания на программирование, разработка и описание макроблок-схемы программы, разработка и описание микроблок-схемы программы, разработка программы в условных адресах, разработка программы в действительных адресах, разработка дополнительных вспомогательных программ и стандартных подпрограмм, необходимых для данной задачи, отладки отдельных частей программы, комплексная отладка программы на контрольном примере; описание программы, разработка контрольного примера.
На основе замечаний к техническому проекту АСУ проводится уточнение постановки и алгоритмизации задачи. Особое внимание уделяется кодам, используемым в данной задаче, значимости реквизитов, объемам входной и выходной информации, а также взаимосвязям задач АСУ.
Контрольный пример
Для проверки правильности алгоритмов решения задачи, правильности отладки программ и реализации задачи на ЭВМ делается контрольный просчет либо приводятся исходные данные и окончательные результаты счета. При этом правильность работы программы оценивается по результатам решения.
сходные данные для контрольного примера могут быть реальными или искусственно созданными числами и должны полностью охватывать все этапы Решення поставленной задачи. Контрольный пример должен быть подобран так, чтобы была обеспечена стыковка задач на основе информационных связей между ними. Для создания искусственного массива исходных данных должны быть даны отправные точки для каждого реквизита. Контрольный пример прилагается к постановке задачи и не входит в состав документации проекта.
Контрольный пример содержит:
- набор всех входных документов, заполненных конкретными данными (для формирования оперативной оперативной информации НСИ и информации, получаемой от других задач);
- контрольные значения накопленной и хранимой для других задач информации;
- формы выходных документов с данными, рассчитанными в полном соответствии с алгоритмом.
В контрольном примере следует учесть максимально возможное количество различных вариантов вычислительного процесса.
Проектирование экономических задач на базе типовых проектных решений
Типизация проектирования экономических задач предусматривает разработку и использование типовых проектных решений (ТПР).
Класс ТПР «Задача» охватывает комплекс алгоритмов и программ, реализующих определенные функции управления в ЛСУП. В зависимости от реализуемых функций управления ТПР этого класса разделены на подклассы — функциональные подсистемы. ТПР по подсистемам представляют собой комплекс задач, содержание которых определяется опытом разработки и внедрения АСУП. Внутренняя структура каждого типового решения строится по модульному принципу. В зависимости от назначения различают модули алгоритма (экономическое обеспечение) и модули программ (математическое обеспечение).
Модуль алгоритма представляет собой часть алгоритма (алгоритм) задачи, характеризующуюся определенной степенью законченности и устойчивости к изменениям и обладающую возможностью как многократного самостоятельного использования, гак и использования в соединении с оригинальным проектным решением при создании АСУП.
Программный модуль — это комплекс программ (программа), реализующих модуль алгоритма, включая процедуры ввода-вывода данных.
Типовые проектные решения по каждой задаче содержат следующие разделы:
- организационно-экономическая сущность задачи;
- исходные данные;
- выходные данные;
- алгоритм решения задачи;
- описание программных модулей.
Использование ТПР класса «Задача» в процессе проектирования подразделяется на следующие этапы:
по задаче и эквивалентному ей по назначению ТПР проводится сравнение форм выходных документов по составу реквизитов со структурой документа с целью определения соответствия форм выходных документов ТПР требуемой в задаче форме. Затем аналогично составляются формы входных документов. При соответствии форм выходных и входных документов ТПР требуемым для решения задачи формам принимается решение об использовании ТПР без доработки.
Если требуемая выходная форма не соответствует рекомендуемой, то может быть получена из выходного массива ТПР, а если входные данные ТПР могут быть введены, то принимается решение о применении ТПР с составлением описания к стандартной программе вывода данных. В противном случае разрабатывается оригинальное проектное решение; на основании блок-схемы, которая содержится в каждой постановке ТПР класса «Задача», определяется окончательное применение ТПР с точностью до модуля. При этом с заказчиком согласовываются формы входных и выходных документов.
По задачам ТПР разрабатываются схемы информационной увязки ТПР и оригинальных решений. Разрабатывается контрольный пример, который служит для проверки правильности алгоритмов решения задачи, программы или отдельных ее частей (модулей); из библиотеки расписанных по модулям программ отбираются необходимые программы, компонуются в пакеты вместе с оригинальными программами и настраиваются на конкретные параметры (значность реквизитов, структура реквизитов, методика представления чисел, конкретные значения точек пользователя и т. д.). Затем подбирается необходимая документация (блок- схемы, инструкции) для каждой программы модуля, составляются инструкции по пакету и просчитывается контрольный пример конкретной задачи.
Пример постановки экономической задачи
Рассматривается математическая мидель задачи нахождения оптимальной годовой программы для мелкосерийного и единичного производства. Введем обозначения:
j - порядковый номер заказа;
i - вид оборудования;
xj - планируемый годовой выпуск изделий j-го заказа;
bj - количество изделий j-го вида в портфеле заказов;
hj - количество изделий /-заказа, затребованных в директивном порядке;
pj - оптовая цена одного изделия заказа;
Р - запланированный объем реализуемой продукции;
aij - трудоемкость изготовления j-го изделия на i-м виде оборудования;
Фj- календарный фонд работы j-го вида оборудования;
dRj - норматив расхода материалов на изготовление j-го вида изделий;
MR - фонд материалов на выпуск изделий;
Zij - норматив заработной платы на изготовление j-го вида изделий на i-м виде оборудования;
Z - годовой фонд заработной платы;
Si - себестоимость j-го изделия.
Задача должна удовлетворять следующим ограничениям:
1. Количество выпускаемых изделий определенного вида не может быть больше количества изделий, имеющегося в портфеле заказов:

2. По отдельным заказам необходимо выпускать изделий не меньше чем задано в директивном порядке:

3. Объем реализуемой продукции не должен быть меньше запланированной величины:
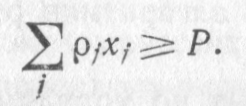
4. Время, затрачиваемое каждым видом оборудования на годовую программу, не должно превышать соответствующих фондов рабочего времени:
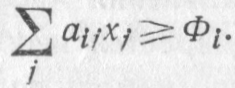
5. Расход материалов на выпуск изделии не должен превышать фондов материалов:
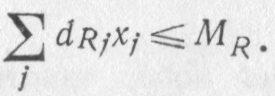
6. Фонд заработной платы, затраченной на производство, не должен превышать установленных фондов заработной платы.
Критерий оптимальности (целевая функция) — минимизация затрат
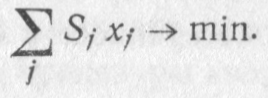
При небольшом числе заказов эта задача решается модифицированным симплекс-методом. Конкретное число заказов п зависит от объема оперативной памяти ЭВМ, от числа видов оборудования га и от числа видов материалов R на программу. Эта зависимость выражается неравенством
(2n+m+R+3)2+(2n+m+R+3)(n+1)≤П,
где П — количество ячеек, отведенное в МОЗУ для исходной и обратном матриц.
В случае больших чисел т, п, R целесообразно воспользоваться методом блочного программирования Данцига — Вольфа. При использовании этого метода количество заказов может достигать нескольких сотен.
Необходимо отметить, что решение модели возможно не по одному, а по нескольким критериям оптимальности, которые можно выбирать в зависимости от различных факторов. Для данной задачи можно предложить еще три критерия, что не исчерпывает всего возможного множества критериев:
- максимальное удовлетворение заказчиков;
- максимальная загрузка оборудования;
- равномерная загрузка оборудования.
Математическое выражение критериев будет иметь следующий вид:
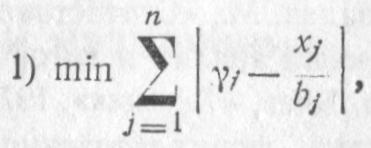
где 0≤γ≤1;
γj— априорная оценка j-го заказчика;
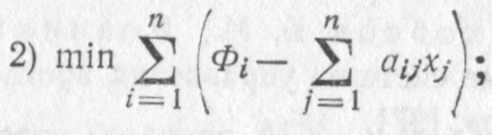
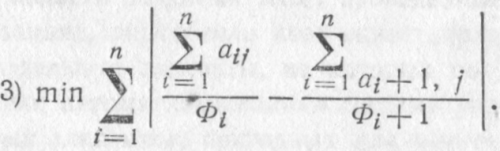
Необходимо отметить, что модульность целевых функций 1 и 3 делает задачу нелинейной.