Формы представления данных

Наиболее часто программы и исходные данные перед вводом в ЭВМ перфорируются на картах. Рассмотрим возможные способы набивки информации на карты.

КОД ХОЛЛЕРИТА

При работе на машинах фирмы IBM стандартным способом перфорации символьной информации на картах является перфорация в коде Холлерита. При этом используются стандартные карты размером 80 на 12. Строки карт пронумерованы сверху вниз в следующем порядке: 12, 11, 0, 1, ... , 9. Каждый столбец предназначен для перфорации одного символа, при этом в строках 12, 11 и 0 перфорируются зонные части, а в позициях 1, ..9 — цифровые части.

Буквам от А до I в коде Холлерита соответствует пробивка в зонной части позиции 12 и в цифровой части — позиций соответственно с 1 по 9, буквам от J до R — пробивка в зонной части позиции 11 и в цифровой части соответственно позиций с 1 по 9, буквам от S до Z — пробивка в зонной части позиции 0 и в цифровой части — позиций с 1 по 9. При кодировании чисел пробивка в зонной части не осуществляется. В цифровой части перфорируется непосредственно требуемая цифра. Заметим, что если в столбце пробита лишь позиция 0, то она не рассматривается как зонная: таким образом кодируется символ, соответствующий цифре 0.

Существуют таблицы кодов Холлерита, каждому символу в них соответствуют номера позиций, которые должны быть пробиты при перфорации данного символа. Например, кодом Холлерита, соответствующим символу К, является 11-2.

Поскольку в дальнейшем нас будут интересовать в основном числа, возьмем произвольное число, например

—137

и рассмотрим способы его представления в различных форматах. В коде Холлерита данное число выглядит следующим образом:

11 = код Холлерита символа «—» в столбце 1

1 = код Холлерита символа «1» в столбце 2

3 = код Холлерита символа «3» в столбце 3

7 = код Холлерита символа «7» в столбце 4

Считается, что число перфорируется, начиная с первого столбца карты.

Код EBCDIC

Я надеюсь, что вы уже заметили сходство между способами представления данных в коде EBCDIC и в коде Холлерита. При считывании карт происходит преобразование данных из кода Холлерита в код EBCDIC; получившаяся после подобного преобразования информация попадает в систему ввода-вывода ЭВМ.

Вспомним, что в коде EBCDIC первой шестнадцатеричной цифрой кода любого символа является код зоны. В процессе считывания карты каждой пробивке в зонной части символа ставится в соответствие определенный код зоны. Четыре последних бита кода EBCDIC получаются преобразованием в двоичную форму номеров позиции цифровой части, в которой осуществлена пробивка. Итак, между кодами зоны и пробивками в зонной части установлено следующее соответствие:

Например, в коде Холлерита символ Q имеет вид 11-8. В коде EBCDIC этот же символ выглядит как D8.

Сформулированные выше положения касаются только соответствия между кодами Холлерита и EBCDIC буквенных и цифровых символов. Аналогичные правила существуют также для знаков пунктуации и специальных символов. Соответствующая таблица, с помощью которой можно производить преобразования, приведена в приложении 3.

Возвращаясь к нашему предыдущему примеру, имеем

Итак, число — 137 в коде EBCDIC выглядит как 60F1F3F7.

Зонный формат

Оставшаяся часть данной главы посвящена в основном способам представления в машине десятичной числовой информации. Одним из основных отличий машинных способов представления числовой информации от более привычных нам является то, что в машине знак числа рассматривается в качестве естественного элемента его внутреннего представления. Например, в случае двоичных целых знаковый бит вообще является частью числа. Напротив, мы больше привыкли к тому, что знак размещается перед цифрами, составляющими непосредственно число. Мы считаем, что число положительно, если перед ним указан знак + (возможно также, что перед числом нет никакого знака). Если же перед числом указан знак —, то считается, что оно отрицательно.

Преобразование числа из кода EBCDIC в зонный формат как раз и отражает это различие в способах представления знака. Для получения зонной формы числа из его кода EBCDIC необходимо код знака поместить в зонную часть символа последней цифры числа, так называемую знаковую зону, а затем заменить начальный код знака нулем. (Впоследствии мы увидим, что при выполнении различного рода преобразования последний шаг не всегда является обязательным). Существуют следующие знаковые коды:

Другими словами, если зонная часть последнего символа кода числа, записанного в зонном формате, содержит С или F, TO число считается положительным. Если же знаковая зона содержит D,TO число — отрицательно.

Мы получили, что кодом EBCDIC числа —137 является 60F1F3F7

Поскольку —137 — число отрицательное, то в качестве кода знака должно выступать D. Соответствующий код должен быть помещен в зонную часть последнего символа кода числа:

D

?

60F1F3X7

Итак, в результате имеем

60F1F3D7

Чтобы быть совсем точными, нам необходимо заменить код знака —(60) на код нуля (F0):

F0F1F3D7

Можно было просто удалить код знака:

F1F3D7

Позднее мы увидим, что при проведении дальнейших преобразований правильный результат можно получить, имея в качестве исходной информации любую из трех последних форм.

Рассмотрим еще несколько примеров. Зонный формат числа

+500

выглядит как

F0F5F0C0

а зонный формат числа

63

как

F6C3

В обоих случаях зонная часть последнего байта содержит С, что указывает на положительность чисел.

Упакованный формат

Вообще говоря, возможно построить ЭВМ, способную выполнять арифметические операции над числами, записанными в зонном формате или даже в коде EBCDIC. Однако нетрудно заметить, что в таком случае около половины всего места, отводимого для записи числа, будут занимать зонные части. Полезную информацию при этом будет нести только содержимое знаковой зоны. Все остальные зоны будут содержать код F. Упакованный десятичный формат — это не что иное, как способ более компактной записи десятичных чисел. Для получения числа в упакованном формате достаточно удалить все не несущие информации зоны из зонного формата десятичного числа. Содержимое знаковой части при этом следует переместить в правый конец числа. Описанный процесс изображен на рис. 15.1.

Итак, число, представленное в упакованном формате, имеет по крайней мере на одну цифру больше по сравнению с его обычной записью. Если в исходном виде число состояло из четного числа цифр, то с левого конца оно дополняется нулем (число всегда должно размещаться в целом количестве байтов).

Мы видели, что в зонном формате число —137 выглядит как

F1F3D7

Для получения упакованного формата код знака перемещается в правый конец числа (можно считать, что меняются местами две последние цифры). Получается

F1F37D

Затем удаляются все зоны, содержащие F:

137D '

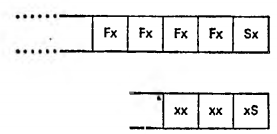
Рис. 15.1. Преобразование из зонного формата в упакованный. Символ х обозначает произвольную десятичную цифру. Символ S — код знака.

Таким образом, нами получен окончательный результат. Аналогично число, записывающееся в зонном формате как

F5F0C0

в упакованном виде выглядит следующим образом:

500С

Если же зонный формат выглядит как

F6F3F2D3

то число в упакованном формате записывается в виде

06323D

В последнем случае число спереди дополнено нулем.

Упакованный формат можно рассматривать как модификацию двоично-десятичной записи числа в коде BCD. В двоично-десятичной записи каждая десятичная цифра представляется группой из четырех битов, при этом содержимое каждой группы попросту есть соответствующая десятичная цифра, записанная в двоичной системе счисления. Например, число 4510 можно представить как

0100 0101,

или как

451в

(в последнем случае использована двоично-десятичная форма записи). Отметим, что двоично-десятичное представление числа в общем случае не совпадает с его двоичным представлением. Имея двоично-десятичную запись числа, уже легко получить его в упакованном формате. Для этого достаточно дополнить двоично-десятичную запись справа кодом знака.

С точки зрения представления чисел в машине упакованный формат является более предпочтительным, чем зонный. В упакованном десятичном числе каждая группа из четырех битов кодирует одну десятичную цифру от 0 до 9. Однако рассмотрение двоичной записи числа показывает, что в ней уже группой из четырех битов может быть закодировано любое число от 1 до 15. Отсюда следует, что упакованный формат хотя и более экономен с точки зрения использования памяти, чем зонный, все же не так эффективен, как обычная двоичная запись числа.

Тем не менее (это будет показано в следующей главе) упакованный формат является очень удобным способом представления числовых данных в машине. Большинство ЭВМ Систем 360 и 370 имеют команды, необходимые для выполнения арифметических операций, а также операций сравнения и пересылки над десятичными числами, записанными в упакованном формате.

Двоичная форма записи

Пожалуй, наиболее употребительным способом представлений как целых чисел, так и чисел с плавающей точкой (см. гл. 19), является двоичная запись. Знакомое нам число — 137 в двоичной форме выглядит как

FFFFFF77

Все описанные выше преобразования: EBCDIC в зонный формат, зонного формата в упакованный и упакованного в двоичную запись — являются обратимыми. Поэтому, имея число, записанное в одном из перечисленных форматов, можно легко получить любой другой его формат. Например, содержимое полного слова

000000631в

в упакованном формате выглядит как

099С

в зонном формате как

F0F9C9

и, наконец, в коде EBCDIC как

F0F9F9

Попрактикуйтесь в проведении подобных преобразований.