Машинный способ выполнения арифметических операций над числами с плавающей точкой очень легко понять, если провести аналогию между ним и обычным способом выполнения арифметических операций над числами, представленными в виде чисел с порядком. Например, 356400 в форме с порядком может быть записано как 3.564 Х105. Вообще число в форме с порядком выглядит как произведение двух чисел, одно из которых является степенью 10. В машинах фирмы IBM числа с плавающей точкой имеют примерно такой же вид, только в качестве основания системы счисления берется не 10, а 16. Число с плавающей точкой в шестнадцатеричной системе записывается как
дробная часть X 16"
Мы требуем, чтобы абсолютная величина дробной части была меньше 1. Число п называется порядком числа с плавающей точкой. (Часто дробная часть называется мантиссой).
Требование, чтобы абсолютная величина мантиссы не превышала 1, означает, что все ее значащие цифры должны располагаться после шестнадцатеричной точки. Например, .СЗАХ162 является представлением числа СЗ.А1в, а .10ЕХ16-3 — представлением числа .00010Е16.
Алгоритм выполнения арифметических операций над числами с порядком в десятичной системе ничем не отличается от соответствующего алгоритма для шестнадцатеричной системы. Для того чтобы сложить два числа, сначала выравнивают их порядки, производя сдвиг мантиссы одного из них, а затем мантиссы складывают. При умножении мантиссы перемножаются, а порядки складываются. Проверьте справедливость следующих равенств:
. 1С2 X 163—. 8Е X 163 = . 1С2 X 163»— .08Е X 163 = . 134 X 163
(.ЗА х 163) X (.42 X 162)= .EF4X 165
Проведение вручную преобразований чисел с плавающей точкой из десятичной системы в шестнадцатеричную достаточно утомительно, но возможно. Например,
С1 16 Х 163=(12х 16-1+1 X 16)-2Х 163= 12 х162+ 1х16=308810
Посмотрим теперь, как выполняются подобные операции машинами фирмы IBM.
Внутреннее представление
Число в форме с плавающей точкой представляет собой совокупность знака, порядка и мантиссы. В машинном представлении чисел с плавающей точкой нулевой бит всегда несет информацию о знаке числа: 0 соответствует плюсу и 1 — минусу. Следующие 7 битов отведены под характеристику, являющуюся внутренней формой представления порядка. Остальное место занимает мантисса.
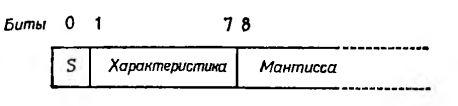
Знак. Числа с плавающей точкой, одинаковые по абсолютной величине, но имеющие разные знаки, отличаются друг от друга во внутреннем представлении лишь содержимым знакового разряда. Заметим, что в случае двоичной целочисленной арифметики дело обстояло совсем не так: отрицательные числа представлялись в дополнительном коде. Для умножения числа, представленного в форме с плавающей точкой, на —1 достаточно лишь изменить значение его знакового разряда. Мантисса чисел с плавающей точкой во внутреннем представлении фактически представляет собой абсолютную величину мантиссы. Умножив С380315Е на —1, мы получим 4380315Е.
Характеристика. Поскольку характеристика представлена 7-раз-рядным двоичным числом, ее значение может находиться в пределах от 00 до 7F16 или от 0 до 12710. Если бы в поле характеристики записывался в явном виде порядок числа, то мы имели бы числа исключительно с положительными порядками. Для того чтобы получить возможность пользоваться и числами с отрицательными порядками, в поле характеристики записывают число, превосходящее истинное значение порядка на 6410. Такое представление порядка называется представлением относительно числа 64. Минимальное значение характеристики равно 00000002. Минимальное значение порядка на 64 меньше, т. е. равно — 64. Аналогично, поскольку максимальное значение характеристики равно 12710, то, значит, в машине могут представляться лишь числа, порядок которых не превышает 6310. Итак, в машине представимы числа с плавающей точкой, находящиеся в интервале от 16-61 до 16+03, т. е. приблизительно от 5.4Х10-78 до 7.2X10'*.
Найти значение характеристики, соответствующее данному значению порядка, можно так: сначала преобразовать исходное значение порядка в двоичную форму, а затем, используя арифметику дополнительных кодов, прибавить к нему 6410 = Ю000002. Например, если порядок равен 1310, то характеристика вычисляется так:
1310+10000002=000 11012+10000002 = 100110112=3B16
Аналогично, если порядок равен — 5, то характеристика
—510+1000000a= 11110112+10000003=01110112=ЗВ1b
Отметим, что знак порядка может быть легко определен по первому биту характеристики: если этот бит равен 1, то порядок положителен, если 0 — то отрицателен. Это, возможно, несколько непривычно, но тем не менее это так.
Мантисса. ЭВМ Систем 360 и 370 предоставляют возможность выполнения арифметических операций над числами с плавающей точкой двух форматов. Короткие числа с плавающей точкой занимают 32 разряда, т. е. полное слово памяти. Под знак и характеристику отведено 8 разрядов; таким образом, короткие числа имеют 24-разрядную мантиссу. Длинные числа с плавающей точкой состоят из 64-х битов, т. е. занимают двойное слово. Мантисса таких чисел содержит 56 битов.
В гл. 2 мы видели, что многие десятичные дроби не могут быть точно представлены в виде конечных двоичных. Например,
110 = .00011001100110011...2 = . 19999999…16
Для того чтобы точно представить подобные числа в машине, требуется бесконечное количество разрядов, так как в двоичной форме они представляются в виде бесконечных периодических дробей. При представлении таких чисел в реальных машинах допускаются ошибки округления.
Конечно, чем больше разрядов отводится для представления числа, тем выше точность этого представления. В связи с этим обычно возникает вопрос, какова точность аппроксимации десятичных дробей двоичными?
Для ответа на этот вопрос выясним, насколько отличаются числа, не совпадающие только в последнем разряде. Если дробные части чисел состоят из N битов, то разница будет 2-N. Изменяя содержимое последнего разряда 4-разрядного дробного числа, мы изменим его величину на 2-4=1/16. Оценить соответствующую величину десятичного приращения можно, решив уравнение
10-x=2-N
Решить это уравнение можно, взяв десятичный логарифм от обеих частей:
— х log10 = ~N log10 2; х = N log10 2
или приблизительно
x=0.3N
Возвращаясь к представлению чисел в виде коротких чисел с плавающей точкой, имеем x=0.3x24=7.2
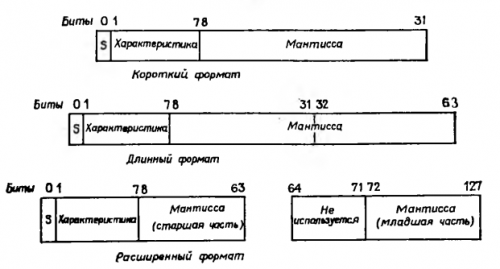
Рис. 19.1. Короткий, длинный и расширенный форматы чисел с плавающей точкой. S — бит знака.
Итак, используя 24 разряда для представления мантиссы чисел, мы получаем относительную точность их машинного представления в пределах 10-7,2. Другими словами, относительная точность представления чисел в случае одинарной точности (короткие числа с плавающей точкой) равна приблизительно 10-7. Аналогичные вычисления показывают, что при операциях удвоенной точности (длинные числа) можно получить относительную точность представления приблизительно 10-18. Мы получили оценки точности, обеспечиваемой при машинном представлении чисел с плавающей точкой. В дальнейшем мы увидим, что ошибки округления, возникающие при использовании арифметики с плавающей точкой, могут быть столь велики, что конечные результаты практически теряют всякий смысл.
Модель 85 Системы 360 и модели Системы 370 позволяют оперировать с числами, представленными в так называемом расширенном формате. С помощью такого формата достигается еще более высокая точность. Число, записанное в расширенном формате, занимает четыре полных слова. Первое двойное слово имеет тот же формат, что и в случае длинного числа. Однако знак и характеристика относятся ко всему 128-разрядному числу. На самом деле для записи числа используются только 120 разрядов, поскольку содержимое полей знака и характеристики второго двойного слова игнорируется. Итак, мантисса таких чисел имеет 128—16=112 разрядов. При этом относительная точность повышается до 10-36.
На рис. 19.1 изображены все форматы представления чисел с плавающей точкой в машинах фирмы IBM. Как же определить число по его внутреннему представлению? Для ответа на этот вопрос число разбивается на три части. Рассмотрим, например, короткое число
Поскольку нулевой бит равен 0, число положительно. Характеристика равна 43,в=6710; вычитая 64, получим значение порядка, равное 3. Мантисса равна .00С00016. Таким образом, искомое значение получится переводом числа
.00С000Х163
в десятичную форму. Окончательно получаем результат
.C00000X 161 = 1210
Аналогично число
А56С429В
отрицательно, поскольку нулевой бит равен 1. Характеристика равна 25lg=3710, т. е. порядок равен —27,0. Получаем, что представленное число равно
—.6С429Вх16-27
Точно так же определяются значения чисел, представленных в двойном и расширенном форматах. Единственное отличие заключается в длине мантиссы.
Нормализация. Число с плавающей точкой называется нормализованным, если первая шестнадцатеричная цифра его мантиссы отлична от 0. На самом деле в нормализованном виде числа представляются наиболее точно, поскольку реально используются все разряды мантиссы. Рассмотрим нормализованное представление в коротком формате числа .2. Оно выглядит так:
40333333
Точность чуть больше чем 10~7. В ненормализованном виде это же число может быть записано, например, как
43000333
В данном случае реально используется всего 12 из 24 двоичных разрядов мантиссы. Теперь уже точность представления оказывается меньше 10-4. Аналогичные рассуждения можно провести относительно длинных и расширенных чисел. Использование ненормализованных чисел обычно ведет к уменьшению общей точности вычислений.
Для нормализации числа нужно выполнят^ последовательные сдвиги его мантиссы на четыре двоичных разряда каждый раз с одновременным вычитанием 1 из характеристики до тех пор, пока первая шестнадцатеричная цифра мантиссы не окажется отличной от 0. Нормализовав длинное число
С5000638 4С8096Е5
получим
С26384С8 096Е5000
Значение характеристики числа во время нормализации уменьшилось на поскольку было выполнено три 4-разрядных сдвига мантиссы. В процессе нормализации младшие разряды заполнились нулями. При выполнении арифметических операций, как мы увидим в дальнейшем, дело обстоит несколько сложнее, чем здесь описано.
Операнды команд с плавающей точкой
Команды арифметики с плавающей точкой бывают форматов RR и RX. Операнд команд формата RX, находящийся в памяти, в случае выполнения операций над числами, представленными в коротком формате, выровнен по границе полного слова. Выполнение операций над числами, представленными в расширенном формате, производится почти исключительно с помощью команд формата RR. В этом случае в качестве операндов выступают так называемые регистры с плавающей точкой (FP). Эти специальные регистры не следует путать с регистрами общего назначения (GP,). FP-регистров всего восемь. Им присвоены номера от 0 до 7. Но только четные регистры могут выступать в качестве операндов команд арифметики с плавающей точкой в случае, когда обрабатываемые числа имеют.короткий или длинный формат. Для выполнения операций над числами, представленными в расширенном формате, можно использовать только регистры 0 и 4. Несоблюдение этих правил приводит к особому случаю спецификации.
Каждый регистр с плавающей точкой является 32-разрядным. Четные регистры содержат байт, представляющий знак и характеристику числа, а также 24 разряда мантиссы. В нечетных регистрах записываются 32-разрйдные части мантисс. Это означает, что каждая пара, состоящая из четного и нечетного регистров с последовательными номерами, может быть использована для хранения числа, представленного в длинном формате. В выполнении операций над короткими числами нечетные регистры не участвуют. Расширенные числа могут находиться либо в регистрах 0—3, либо в регистрах 4—7.
Регистры, использующиеся в качестве первых операндов в RR- или RX-командах арифметики с плавающей точкой, играют роль накопителей, аналогично тому как это имеет место в командах целочисленной арифметики.
Арифметика
Порядок машинного выполнения операций над числами с плавающей точкой мало чем отличается от порядка ручного выполнения этих операций. Единственным серьезным отличием является то, что числа, представленные в машине, имеют фиксированную длину. Описываемые ниже алгоритмы применимы ко всем видам внутреннего представления чисел с плавающей точкой.
Непосредственному выполнению сложения и вычитания предшествует так называемая предварительная нормализация. При этом сравниваются характеристики операндов. Если они равны между собой, то производится сложение или вычитание мантисс в зависимости от выполняемой операции и содержимого знаковых разрядов операндов. Если же характеристики различны, то происходит их выравнивание. Меньший порядок увеличивается до значения большего, и одновременно происходит сдвиг мантиссы соответствующего числа с меньшим порядком. Увеличению порядка на 1 соответствует сдвиг мантиссы вправо на 4 разряда. При этом последняя выдвинутая за пределы разрядной сетки шестнадцатеричная цифра сохраняется. Процесс продолжается до тех пор, пока значения характеристик не совпадут. После этого выполняется сложение или вычитание мантисс.
Мы можем потребовать, чтобы результат сложения или вычитания нормализовался или не нормализовался. При нормализации результата сохраненная шестнадцатеричная цифра перемещается в младшие разряды мантиссы. Таким образом, достигается несколько большая точность, чем та, которая гарантируется использованием короткого, длинного или расширенного форматов соответственно.
Вычислим, например, сумму двух коротких чисел с плавающей точкой.
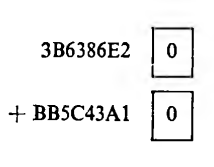
Значения характеристик обоих чисел совпадают и равны ЗВ1в. Следовательно, предварительную нормализацию в данном случае выполнять не нужно. Первоначально дополнительные младшие разряды обоих чисел содержали нули. Поскольку преднормализация, а следовательно, и сдвиги мантисс не выполняются, то перед непосредственным началом сложения в этих разрядах также будут нули. Второе число является отрицательным, поэтому его мантисса вычитается из мантиссы первого числа. Нормализованная сумма выглядит так:
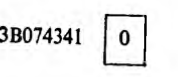
Сложение
4381СА38 + 46В22С21
требует предварительной нормализации, поскольку значения характеристик слагаемых — разные. Меньшим является значение характеристики первого числа, в процессе нормализации его мантисса будет сдвинута на три позиции вправо:
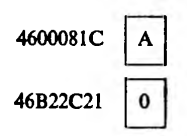
В результате сразу же получится нормализованное число
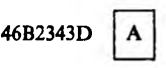
При умножении также производится предварительная нормализация операндов. Значение характеристики произведения равно сумме значений характеристик сомножителей минус 4016. Производится умножение мантисс, и при необходимости результат нормализуется. Вычислим, например, произведение
45300000
X 4С042А31
Второй сомножитель не нормализован, поэтому его мантисса сдвигается на один разряд влево и одновременно значение характеристики уменьшается на 1. Значение характеристики произведения
45300000
X 4В42А310
вычисляется следующим образом:
45+4В—40=50
Произведение мантисс равно
300000 х 42АЗ10=ОС7Е93000000
Итак, предварительно результат записывается в виде
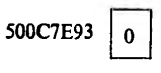
Нормализация дает
4FC7E930
В данном случае первая, выходящая за пределы разрядной сетки, цифра произведения есть 0. Если бы это было не так, то она добавлялась бы к значению произведения для повышения точности вычислений. В данном случае дополнительная цифра есть 0, поскольку один из операндов оказался нормализованным.
Деление чисел с плавающей точкой также начинается с нормализации. Значение характеристики делителя вычитается из значения характеристики делимого и к результату добавляется 4010:
характеристика частного = характеристика делимого — характеристика делителя + 4016
Нормализация частного иногда не требуется, однако возможна ситуация, когда мантисса частного после выполнения деления сдвигается на одну позицию вправо.
Разделим, используя арифметику с плавающей точкой, 0.3x162 на 0.9Х163. Иначе говоря, требуется вычислить частное:
42300000
?43900000
Характеристика частного вычисляется следующим образом:
42—43 +40 =82—43 = 3F
что соответствует порядку —1. Результатом деления мантисс является бесконечная дробь .5555555..., т. е. 1/3 в шестнадцатеричной форме. Поэтому частное в машинном представлении будет выглядеть так
3F555555
Констатны с плавающей точкой
Константы короткие, длинные и расширенные фигурируют в языке ассемблера как константы типовЕ, D и L соответственно. Значения констант записываются в десятичной форме. Например, с помощью предложений
SINGDC Е'.ООЗ'
DOUB DC D'.003'
LONG DC L'.003'
определяются три константы, имеющие различные форматы, но одно и то же значение, а именно .003. Е-константы автоматически выравниваются по границам слов, a D- и L-константы выравниваются по границам двойных слов.
При желании константы можно записывать непосредственно в форме с плавающей точкой, указывая в них соответствующие степени 10. Степень 10 записывается в виде буквыЕ со следующим за ней значением показателя.
Например, предложением
AVOG DC D'6.023E23'
определяется длинная константа с плавающей точкой со значением 6.023 X 10м, а предложением
NANO DC E'l.E — 9'
— константа со значением 10~9.
Значения порядков можно задавать другим способом, указывая их непосредственно перед значением самой константы. Следующие два предложения эквивалентны двум предшествующим:
AVOG DC DE23'6.023'
NANO DC ЕЕ—9'1.'
Значение показателя, выведенное за апострофы, относится ко всем числам, указанным внутри их. Например,
THOU DC ЕЕ+4'1.,2.,3/
является определением трех коротких констант, которые будут загружены в память, начиная с ячейки THOU. Значениями этих констант являются соответственно 10000, 20000, 30000.
Литералы, соответствующие константам с плавающей точкой, записываются аналогично. Например, по команде
DE 4, = ЕЕ — 9'1/
содержимое регистра 4 делится на 10~9.