Логика и её машинная реализация

Логика по существу является наукой о методах распознавания истинности или ложности отдельных высказываний. Символическая логика занимается изучением функций от переменных, принимающих одно из двух значений: «истина» или «ложь». Возможные значения функций принадлежат тому же множеству. Утверждения и доказательства символической логики обычно базируются на так называемой булевой алгебре, представляющей собой множество правил, отношений и операций, использующихся для определения истинности высказываний. В этом разделе мы познакомимся с операциями булевой алгебры, а также с некоторыми другими, имеющими большое применение в приложениях. Затем мы рассмотрим вопросы, связанные с конкретной реализацией логики в ЭВМ.

ОПЕРАЦИИ СИМВОЛИЧЕСКОЙ ЛОГИКИ

Нам будет достаточно рассмотреть четыре логические операции. К числу таких операций принадлежат И (AND), СЛОЖЕНИЕ ПО МОДУЛЮ 2 (exclusive OR — XOR), ИЛИ (OR) и НЕ (NOT). Первые три операции являются бинарными, т. е. имеют по два аргумента и одно значение. Операция НЕ является унарной операцией, она напоминает унарную арифметическую функцию sign.

Операция И (AND). В английском языке слово И (AND) используется для связки двух простых предложений в сложное. В логике И имеет приблизительно тот же смысл, однако здесь существуют точные правила установления истинности результирующего предложения. Предположим, что предложение имеет вид

[предложение 1] и [предложение 2]

и что предложения 1 и 2 могут независимо друг от друга принимать по одному из значений «истина» или «ложь». Пусть А является значением предложения 1, а В — значением предложения 2. В этом случае результирующее предложение можно записать так:

A AND В

Нас интересует, в случае каких А и В результирующее предложение окажется истинным. Здесь можно воспользоваться аналогией с применением И (AND) в обычном английском языке. Результирующее предложение

[предложение 1] и [предложение 2]

истинно, когда оба предложения 1 и 2 истинны. Во всех остальных случаях значением сложного предложения является «ложь».

Пусть в качестве предложения 1 выступает предложение

«бит есть двоичная цифра»

а в качестве второго предложения — предложение

«капуста есть овощ»

Сложное предложение

[предложение 1] и [предложение 2]

очевидно, истинно. С другой стороны, если бы в качестве предложения 2 выступало предложение

«капуста есть булыжник»

то результирующее предложение

[бит есть двоичная цифра] и [капуста есть булыжник]

имело бы ложное значение.

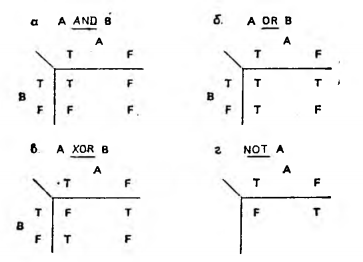
Рис. 14.1. Матрицы истинности для логических операций AND, OR, XOR и NOT. (Здесь Т (True) означает «истина», F (False) — «ложь».)

Аналогично, если А и В — логические переменные, то выражение

A AND В

истинно лишь в случае истинности обоих переменных. Более наглядно это можно записать так:

Более компактный способ представления логических операций состоит в использовании матрицы истинности. На рис. 14.1, а приведена матрица истинности операции И. В верхней строке указываются всевозможные значения переменной А, в крайнем левом столбце — значения переменной В. Значение A AND В отыскивается на пересечении строки и столбца, помеченных значениями соответственно В и А.

Операция ИЛИ (OR). Операции типа ИЛИ не имеют в английском языке двух разных слов для своего обозначения. В английском языке обе они имеют эквивалент OR. Что именно имеется в виду, зависит от контекста. Например,

(предложение 1) или (предложение 2) или и то и другое

соответствует операции OR. Случай истинности обоих предложений здесь учитывается. Результатом выполнения операции ИЛИ является «истина», если значение, по крайней мере, одного аргумента есть «истина».

Лишь тогда, когда А и В одновременно ложны, результатом операции является «ложь».

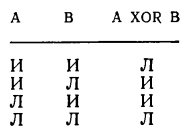
Операция СЛОЖЕНИЕ ПО МОДУЛЮ 2(XOR).XOR (ИСКЛЮЧАЮЩЕЕ ИЛИ) исключает возможность одновременной истинности обоих аргументов. Аналогом XOR может служить такая конструкция обычного языка:

одно из двух: (предложение 1) или (предложение 2) но не оба

Другими словами, A XOR В принимает значение «истина» только в том случае, когда один из аргументов, А или В, есть «истина». В случае истинности обоих значение A XOR В есть «ложь».

Операция НЕ (NOT). Применение НЕ к некоторой переменной дает просто ее логическое дополнение. Если А есть «истина», то NOT А — «ложь», и наоборот, если А — «ложь», то NOT А — «истина».

Реализация логики

Итак, в символической логике переменные, входящие в логические предложения, могут принимать два значения: «истина» и «ложь». Однако здесь важно только то, что каждая переменная может принимать два значения, какие именно — «ложь» и «истина», 0 и 1 или какие-либо другие — безразлично. Поскольку ЭВМ имеют дело с числами, логические значения в них обычно представляются нулем и единицей. На рис. 14.2 приведены уже рассмотренные матрицы истинности в терминах 0 и 1.

Современные ЭВМ используют двоичную систему. Существует точка зрения, согласно которой единственное, что делает ЭВМ,— это логические операции над двоичными числами.

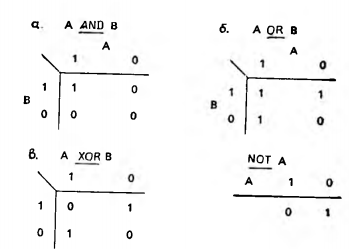
Рис. 14.2. Таблицы истинности логических операций, использующие двоичные числа 0 и 1 для представления логических переменных.

При этом ЭВМ рассматривается как набор переключателей, каждый из которых находится в одном из двух состояний, И или Л, 0 или 1. Все эти переключатели связаны с логическими операторами, или вентилями, которые, открываясь, вызывают выполнение над входными данными описанных логических операций. В результате получаются значения, использующиеся в качестве входных для других вентилей, и т. д. Например, сумма двух одноразрядных двоичных чисел может быть представлена так:

S = (NOT A AND В) OR (A AND NOT В)

С = A AND В

С в данном случае — бит переноса. (Операторы NOT выполняются раньше остальных в рассматриваемом выражении.) Логическая схема вычисления суммы схематически изображена на рис. 14.3.

Все арифметические операции в машине выполняются подобным образом. В принципе, возможно построить ЭВМ, в которой единственными командами для выполнения арифметических операций были бы логические команды и команды сдвига, подобные тем, которые описаны в данной главе. Сложение, вычитание и другие арифметические операции могут быть сведены к последовательности логических операций и сдвигов и, таким образом, могут быть запрограммированы.

В машинах Систем 360 и 370 минимальной адресуемой единицей ин-формации является байт. При выполнении логических операций над байтами или более крупными единицами на самом деле производятся последовательные поразрядные действия. Каждый раз в качестве операнда выступает один двоичный разряд.

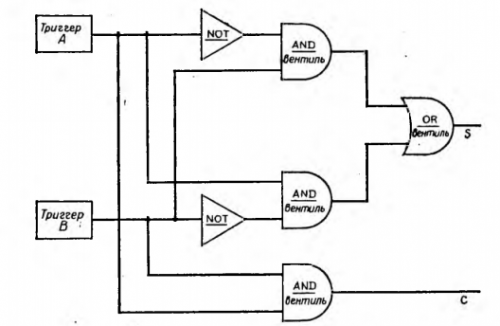
Рис. 14.3. Логическая диаграмма схемы вычисления суммы S и переноса С для двоичных цифр А и В.

Например, если байты А и В имеют соответственно вид

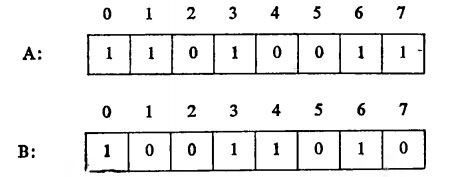
то после выполнения машинной операции A AND В получится следующий результат:

Выполнение операции проходило так:

А В

бит 0 1 1 1 AND 1=1

бит 1 1 0 1 AND 0 = 0

бит2 0 1 0 AND 1 =0

бит 3 1 1 1 AND 1 = 1

Аналогично была получена вторая половина байта. В случае тех же самых исходных А и В операция A OR В дает следующий результат:

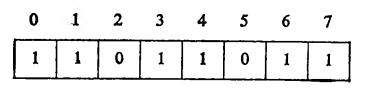
A XOR В:

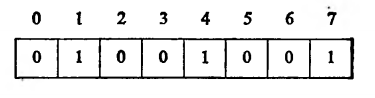
NOT А:

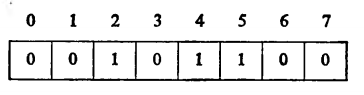
В рассмотренных нами примерах логические операции производились над байтами. Совершенно аналогично можно определить операции над единицами большей длины. Если в качестве операндов используются полные слова, то, очевидно, результат также является полным словом, и каждый его бит получается применением логической операции к соответствующим битам операндов.

Логические операции часто используются для установки в двоичные разряды необходимых значений. Операция И позволяет заносить в соответствующие разряды нули, операция ИЛИ — единицы, Сложение по модулю 2 — получать логические дополнения. Ниже описаны способы получения подобных результатов, которые, впрочем, легко вывести из таблицы истинности.

1. Для установки в данный разряд нуля необходимо его логически умножить на 0 (операция И носит название логического умножения). Умножение на 1 не меняет исходного значения.

2. Для установки в данный разряд единицы его необходимо логически сложить с 1 (операция ИЛИ иначе называется логическим сложением). Сложение с 0 не меняет исходного значения.

3. Для получения логического дополнения данного бита необходимо сложить его по модулю 2 с 1. Сложение по модулю 2 с 0 не меняет исходного значения.

Предположим, что требуется, не изменяя остальные 7 битов байта, присвоить пятому биту значение 1. Для этого достаточно логически сложить исходный байт с байтом, содержащим

00000100₂

Мы можем одновременно изменять значения нескольких битов. Например, логическое умножение данного байта на 10101010₂ установит все нечетные биты равными 0, оставив все четные без изменения. Подобным образом сложение по модулю 2 некоторого байта с 11110000₂ не изменяет второй половины байта, устанавливая первые 4 бита равными их дополнениям.

Отметим, что список команд, включающий команды И, ИЛИ и ИСКЛЮЧАЮЩЕЕ ИЛИ, нет необходимости дополнять командой НЕ. Вычислить дополнение можно, просто сложив по модулю 2 исходное значение с 1.

В результате выполнения команды арифметического сдвига вправо

SRA 11,3

(сдвиг производится на 3 разряда) получится освободившиеся разряды

(11) =0000 0010 0100 0110 1000 1010 1100 1111

Получившееся число равно частному от деления исходного содержимого регистра 11 на 8, что и требуется.

Если же исходное содержимое регистра 11 было несколько иным:

(11) = 1100 1011 1010 1001 1000 0111 0110 0101

то в результате выполнения той же команды получилось бы (11) = 1111 1001 0111 0101 0011 0000 1110 1100

освободившиеся разряды

Мы, следовательно, снова получили деление на 8.

Знаковый бит не сдвигается и при арифметическом сдвиге влево (умножении). Знак результата поэтому совпадает со знаком исходного числа. Освобождающиеся разряды заполняются нулями. Например, если

(11)=0000 0010 0100 0110 1000 1010 1100 1111

то после выполнения арифметического сдвига на 3 разряда влево

SLA 11,3

получим

(11) = 0001 0010 0011 0100 0101 0110 0111 1000

освободившиеся разряды

Если же вначале было

(11) = 1110 1011 1010 1001 1000 0111 ОНО 0101

то выполнение команды

SLA 11,2

даст результат

(11) = 1010 1110 1010 0110 0001 1101 1001 0100

освободившиеся разряды.

Заметим, что в данном случае арифметический сдвиг эквивалентен логическому (SLL 11,2). Разница заключается лишь в том, что если бы мы попытались произвести арифметический сдвиг не на 2, а на 3 разряда, то был бы зафиксирован особый случай переполнения арифметики с фиксированной точкой, тогда как логический сдвиг на 3 разряда влево содержимого регистра 11

SLA 11,3

возможен и дал бы результат

(11) =0101 1101 0100 1100 0011 1011 0010 1000

освободившиеся разряды.

При этом, однако, был бы получен бессмысленный с точки зрения умножения на степень двойки ответ.

При выполнении арифметических сдвигов признак результата устанавливается точно так же, как и при выполнении уже рассмотренных нами команд сложения и вычитания. Итак, признак результата при арифметических сдвигах вырабатывается по следующим правилам:

Рассмотрим пример использования команд арифметического сдвига. Следующая последовательность команд умножает содержимое регистра 5 на 10:

LR 7,5 ЗАСЛАТЬ (5) В РЕГ.7

SLA 5,1 УМНОЖИТЬ (5) НА 2

SLA 7,3 УМНОЖИТЬ ЧИСЛО НА 8

AR 5,7 СЛОЖИТЬ ПОЛУЧИВШИЕСЯ РЕЗУЛЬТАТЫ

Совершенно точно так же, как двойные логические, существуют двойные арифметические сдвиги. Эти сдвиги тоже выполняются над содержимым двух последовательных регистров, первый из которых является четным. Считается, что в регистрах записано единое 64-разрядное целое. Сдвиг производится на число разрядов, определяемое последними шестью битами суммы D2+(B2). Признак результата при этом вырабатывается в полном соответствии с правилами, уже описанными для команд обычного арифметического сдвига. При выполнении двойного сдвига влево может быть зафиксирован особый случай переполнения арифметики с фиксированной точкой.

______________________________________________________________

Первая команда выполняет сдвиг 63-разрядного числа, находящегося в регистрах R1 и R1 + 1, вправо как единого целого. Биты, выносящиеся из разрядной сетки (младшие биты (R1 + 1)), теряются. Содержимое младших разрядов регистра R1 переносится в старшие разряды регистра R1-И. В каждый из освобождающихся разрядов устанавливается знаковый бит.

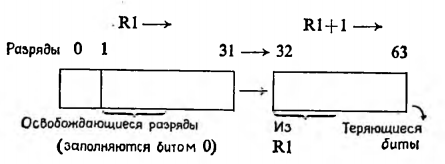
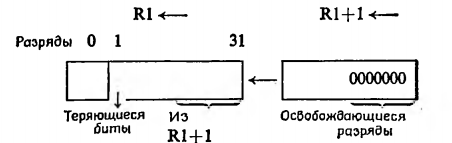
При выполнении второй команды теряются разряды, выносящиеся за пределы разрядной сетки влево (напомним, что содержимое разряда

0 регистра не участвует в сдвиге). Содержимое старших разрядов регистра R1 + 1 становится содержимым младших разрядов регистра R1. Освобождающиеся разряды (в данном случае они освобождаются, начиная с правого конца R1 + 1) заполняются нулями.

Предположим, что

(4) = 1111 1110 1101 1100 1011 1010 1001 1000

(5) =0111 0110 0101 0100 0011 0010 0001 0000

Выполнение команды

SLDA 4,3

даст

(4) = 1111 0110 1110 0101

(5) = 1011 0010 0101 0001

тогда как выполнение команды

SRDA

даст

(4) =1111 1111 1111 0110

(5) = 1100 0011 1011 0010