Объекты данных - Представление знаний

Контрольные вопросы и задания

Для отображения объектов применяются разнообразные структуры. Простые объекты программируются стандартными типами данных. Структура считается более сложной единицей. Она состоит из функтора и аргументов. Функтор есть имя связи, в которую включены аргументы. Например, структура

have(john,computer)

определяет, что Джон имеет компьютер. Функтором здесь служит have, а двумя аргументами — john и computer. Аргументами функтора могут быть константы, переменные и другие структуры. В частности, мы можем создать более сложную и более определенную структуру, например:

have(john,computer(dell,386))

Вторым аргументом мы сделали структуру со своими вариантами. Эта структура описывает конкретный компьютер. Функтором здесь является computer, а аргументами — dell и 386.

Prolog позволяет использовать объекты, содержащие другие объекты.

Например, факты:

owns  (john,   book   ("From Here to Eternity", "James Jones")).
имеет (джон, книга ("Взгляд в будущее", "Джеймс Джоунс")).

owns (john,   horse (blackly )).
имеет(джон, лошадь(черная)).

Здесь используются сложные объекты:

book ("From Here to Eternity", "James Jones")

horse(blackly).

Если записать два факта:

owns (john, "From Here to Eternity").
owns (john,  blacky).

то непонятно: "blacky" — это название книги или имя лошади. Для различения объектов используется функтор. Функтор — первый элемент сложного объекта.

Рассмотрим объявление сложных объектов.

В общем случае объявление области типов объектов будет следующим:

domains
domain=alternative1(D,D...);alternative2(D,D...);

где «alternative1» и «alternative2» — равноправные, но различные функторы; (D, D...) — список типов объектов, стандартных или определяемых пользователем.

Покажем, как можно использовать структуры для представления геометрических объектов. Точка в двумерном пространстве определяется двумя координатами; отрезок определяется двумя точками.

domains 
 point=pset(real, real) 
 line=line(point, point) 
 predicates 
 vert(line) 
 horiz(line) 
 clauses 
 vert (line(pset(X, Y), pset(X, Y1))). 
 horiz (line(pset(X1,Y), pset(X1,Y))). 
 
 goal vert(line(pset(1,1), pset(1,2))). 
 yes 
 goal horiz(line(pset(1,1), pset(2,Y))). 
 Y=1

Cоставим программу, позволяющую заполнить структуру с помощью предикатов ввода .

domains 
 person = p(name, age, telno, job) 
 age = integer 
 telno, name, job = string 
 predicates 
 readperson(person) 
 run 
 goal run. 
 clauses 
 readperson(p(Name, Age, Telno, Job)) :- 
 write("Ваше имя ? "), readln(Name), 
 write("Работа ?"), readln(Job), 
 write("Возраст ?"), readint(Age), 
 write("Номер телефона ?"),readln(Telno). 
 run :-readperson(P), nl, write(P), nl, nl, 
 write("закончить ввод (д/н) "), 
 readchar(Ch), Ch='д' . 
 run :-nl, nl, write("повторите снова"), nl, nl, 
 run.

Рекурсия может быть использована для описания объектов, в которых количество элементов заранее не известно.

Например, определить объект, который определяет имена всех учеников в классе, если заранее не известно количество учеников в классе. Следует пошагово объявить объекты, описывающие класс.

Начнем с описания пустого класса:

classlist = empty

Далее добавим рекурсивное описание:

classlist = class (name, classelist)

Таким образом, описание объекта будет следующим:

class(peter, X).

Это означает, что «peter» будет первым элементом в «classlist». X соответствует оставшейся группе учеников без «peter». Класс из двух учеников может быть описан следующим образом:

class(peter, class(james, empty))

Класс из трех учеников:

class(andrew, class(peter, class (james, empty)))

Сложный объект:

class(name, classlist)

содержит функтор «class» и аргументы:

name – имя ученика в классе;
classlist – оставшиеся ученики в классе.

Итак, область объявления будет иметь вид:

domains
classlist = class(name,classlist);empty

Для числовых данных можно задать следующую область определения:

integerlist = list(integer,integerlist);empty

Рассмотрим представление двоичных деревьев.

Двоичное дерево либо пусто, либо состоит из трех частей:

корень;
левое поддерево;
правое поддерево.

Корень может быть чем угодно, а поддеревья должны сами быть двоичными деревьями.

domains
type = integer
tree = tree(type,tree,tree); nil

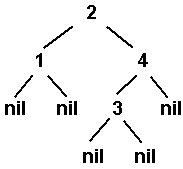
Рис. 12.3. Двоичное дерево

Дерево, представленное на рис. 13, выглядит как

tree(2,tree(1,nil,nil),tree(4,tree(3,nil,nil),nil)).

Определим отношение принадлежности элементу двоичному дереву. Отношение member_tree можно определить при помощи следующих правил:

Х есть вершина дерева T, если

корень дерева T совпадает с Х, или

Х — это вершина из левого поддерева, или

Х — это вершина из правого поддерева.

predicates
member_tree(type,tree)
clauses
member_tree(X,tree(X,_,_)).
member_tree(X,tree(_,L,_)) :-
member_tree(X,L).
member_tree(X,tree(_,_,R)):-
member_tree(X,R).

Будем говорить, что непустое дерево упорядочено слева направо, если

все вершины левого поддерева L меньше Х;
все вершины правого поддерева R больше Х;
все поддеревья упорядочены.

Улучшим процедуру поиска элемента в дереве. Чтобы найти элемент Х в дереве Т, необходимо:

если Х — это корень Т, то считать, что Х уже найден, иначе
если Х меньше, чем корень дерева Т, то искать Х в левом поддереве, иначе
искать Х в правом поддереве;
если дерево Т пусто, то поиск терпит неудачу.

domains 
 id=integer 
 tree=tree(id, tree, tree); nil 
 predicates 
 lookup(id, tree) 
 clauses 
 lookup(X, tree(X,_,_)). 
 lookup(X, tree(K,L,R)) :- X < K, 
 lookup(X,L). 
 lookup(X, tree(K,L,R)) :- lookup(X,R). 
 Покажем, как использовать lookup. 
 predicates 
 a(tree) 
 clauses 
 a(tree(2,tree(1,nil,nil),tree(4,tree(3,nil,nil),nil))). 
 
 goal a(T), lookup(1, T). 
 
 T=tree(2,tree(1,nil,nil),tree(4,tree(3,nil, nil),nil)) 
 1 Solution

Определим отношение, позволяющее добавлять элементы в дерево. Реализуется при помощи правил:

результат добавления элемента Х к пустому дереву есть дерево tree(X, nil, nil);
если Х совпадает с корнем дерева Т, то Т1=Т (не допускается дублирования);
если корень дерева Т больше, чем Х, то Х вносится в левое поддерево Т;
если корень дерева Т меньше, чем Х, то Х вносится в правое поддерево Т.

domains
 id=integer 
 tree=tree(id,tree,tree); nil 
 predicates 
 add(id,tree,tree) 
 clauses 
 add(X, nil, tree(X, nil, nil)). 
 add(X, tree(X,L,R),tree(X,L,R)). 
 add(X, tree(K,L,R),tree(K,L1,R)) :- K>X, 
 add(X,L,L1). 
 add(X, tree(K,L,R),tree(K,L,R1)) :- K<X, 
 add(X,R,R1). 
 
goal T1=nil, add(1, T1, T2), add(2, T2, T3), add(3, T3,T4), add(5, T4, T5). 
 
 T1=nil, 
 T2=tree(1,nil,nil), 
 T3=tree(1,nil,tree(2,nil,nil)), 
 T4=tree(1,nil,tree(2,nil,tree(3,nil,nil))), 
 T5=tree(1,nil,tree(2,nil,tree(3,nil,tree(5,nil,nil)))) 
 1 Solution

Контрольные вопросы и задания

Дайте определение функтору.
Дайте определение главному функтору.
Какие стандартные типы определены в Prolog?
Сформулируйте алгоритм унификации.
Дайте определение бинарному дереву.
Определите понятие двоично-троичный справочник.
При решении каких задач применяются структуры данных?
При решении каких задач применяются двоичные деревья?

Определите, является ли приведенная запись структурой.

человек(пол, возраст, работа, место жительства).
одежда(зимняя(шуба, шапка, валенки), летняя(купальник, сарафан, туфли)).
54 год (возраст).
ткань (ситец,батист, шелк, драп).
бытовая_техника (кухонный_комбайн микроволновая_печь тостер).
драгоценные камни (алмаз, сапфир, аметист, топаз).
знаки_зодиака(‘овен, телец, близнецы, рак, лев, дева, весы, скорпион,
стрелец, козерог, водолей, рыбы’).
породы_собак(колли, овчарка, дог, сербернар, лайка ).
Английский_алфавит.
блюда (пельмени, борщ, вареники, котлеты, суп, жаркое).
 
меню (горячие_блюда (рассольник, уха, борщ), 
холодные_блюда (мясной_салат, окрошка, венегрет), 
напитки (чай, кофе, коктейль)).
 
витамины ( А(морковь, тыква, помидор, абрикос, укроп), 
Д(печень, треска, рыбий жир, сельдь), 
Е(соя, облепиха, горох), 
К(капуста, шпинат, салат), 
С(шиповник, апельсин, чёрная смородина, лимон)).
 
19:00 (время).
деревья (лиственные(дуб, берёза, осина, тополь), 
хвойные(ель, кедр, пихта, сосна)).
 
материки(‘Европа’, ‘Азия’, ‘Африка’, ‘Антрактида’, ‘Австралия’).

Опишите процесс сопоставления структур.

праздник(новый_год, рождество) и праздник(Что, Рождество);
мяч(прыгать) и мяч(Что_делать)
игрушка(машина, деревянная) и игрушка(машина, Какая);
комната(стена, потолок, пол) и комната(Что, потолок, Что);
дерево(Что, лиственное) и дерево(берёза, Какая);
медведь(бурый, белый) и медведь(Какой, Какой).