Сущность десятичной арифметики

До сих пор мы ограничивались лишь рассмотрением некоторых команд, использующих десятичные операнды. Теперь постараемся разобраться, что же на самом деле подразумевается под десятичной арифметикой. До сих пор десятичные операнды записывались нами в шестнадцатеричном представлении именно в том виде, в котором они находятся в памяти машины. Например, число 137D имеет следующий вид в памяти:

0001 0011 0111 1101

При выполнении операций десятичной арифметики каждая шестнадцатеричная цифра числа, за исключением кода знака, ведет себя как десятичная цифра. При выполнении арифметических операций машина использует те же приемы, например, заем единицы из старшей позиции, перенос из младшего разряда в старший и т. д., что и люди, выполняющие вычисления вручную. Результатом выполнения десятичной операции сложения чисел 137D и 200С будет

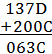(десятичное)

или

200+ (—137)=63.

Однако если те же самые числа рассматривать как двоичные, то результат будет иным:

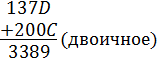
Конечно, этот результат, снова рассматриваемый как десятичное число, не дает никакого представления об искомой десятичной сумме. Если иметь в виду шестнадцатеричную форму записи упакованных десятичных чисел, то результат выполнения операции десятичной арифметики выглядит так же, как если бы мы самостоятельно провели необходимые вычисления. Информация в ЭВМ в любом случае представляется в виде наборов из нулей и единиц. При выполнении команд десятичной арифметики содержимое каждой группы из четырех двоичных разрядов операнда, за исключением последней, рассматривается как десятичная цифра.

Использование десятичной арифметики

Возможно, вы находитесь в некотором недоумении относительно того, зачем понадобилась нам десятичная арифметика, когда уже существуют способы выполнения аналогичных операций над двоичными числами. Многие ЭВМ не обладают дополнительными возможностями десятичной арифметики. Однако в некоторых ситуациях использование десятичной арифметики позволяет более эффективно и с большим удобством достичь желаемых результатов.

Сначала сравним пределы, в которых могут производиться вычисления при использовании двоичного и десятичного способов представления чисел. Максимальной единицей памяти, отводимой для записи двоичных чисел, является 32-разрядное полное слово. Таким образом, соответственно наибольшим и наименьшим числами, представленными в машине при использовании двоичных чисел, являются 2147483647 и —2147483648. Во многих случаях, например при управлении циклами или при индексации, этого вполне хватает. С другой стороны, как мы впоследствии убедимся, в принципе возможно использовать десятичные операнды, имеющие до 31 десятичной цифры. Абсолютная величина таких операндов может достигать 1031 —1, т. е. числа, состоящего из тридцати одной девятки. При выполнении коммерческих расчетов иногда требуется оперировать с числами порядка 10 миллионов и более. При этом, кроме того, требуется высокая точность вычислений. Здесь двоичная арифметика без применения специальных под-программ, позволяющих работать с числами повышенной разрядности, бессильна.

В отличие от двоичной арифметики, где существуют строгие ограничения на длину операндов (допустимыми операндами являются полуслово и полное слово), в десятичной арифметике таких ограничений нет. Здесь позволяется использовать операнды с переменной длиной. Это, в частности, означает, что длина числа может меняться в процессе десятичной обработки. Это свойство не столь уж важно, скажем, при управлении циклами, однако оно может быть удачно использовано при выполнении коммерческих расчетов.

Мы уже говорили о том, что наиболее экономной с точки зрения объема необходимой памяти формой записи числовой информации является двоичная форма. Минимальным же операндом команд двоичной арифметики является полуслово. Так как операнды команд десятичной арифметики могут быть и однобайтовыми, то в некоторых случаях ее использование позволяет достигать существенной экономии памяти, несмотря на то что упакованный десятичный формат с точки зрения экономии памяти не является самым совершенным.

Основным преимуществом использования двоичной арифметики является высокая скорость вычислений. В одной из типичных моделей Системы 360 выполнение операции десятичного сложения АР происходит в шесть с половиной раз медленнее, чем выполнение аналогичной двоичной операции AR1). В связи с тем то AR является двухбайтовой командой, а АР — шестибайтовой, в некоторых других ЭВМ Системы 360 отношение скоростей выполнения этих же команд еще больше. Здесь же, тем не менее, необходимо отметить, что команда преобразования десятичных чисел в двоичные, а также команда обратного преобразования выполняются достаточно долго (время выполнения каждой из них примерно в 12 раз больше, чем время выполнения команды AR). Таким образом, если используемое в процессе вычислений значение должно быть предварительно введено в ЭВМ или по завершении процесса результаты должны быть распечатаны, то в случае использования двоичной арифметики необходимо также учесть время, требуемое на проведение соответствующих преобразований. Кроме того, все команды десятичной арифметики являются командами формата SS, а это означает, что оба их операнда находятся в памяти. В данном случае для выполнения сложения, например, двух чисел, хранящихся в памяти, необходимо выполнить лишь одну команду. Если же используется двоичная арифметика, то для выполнения аналогичной операции требуется включение в программу группы из трех команд: загрузки, сложения и записи в память.

Таким образом, на выбор типа арифметики для данного применения влияют несколько факторов. Сравнительная характеристика команд той и другой арифметики дана в табл. 16.1. Сама по себе двоичная арифметика позволяет достичь большей скорости вычислений по сравнению с десятичной, однако неизбежны и некоторые потери, которые, однако, носят скрытый характер (потери на проведение преобразований данных). Двоичная арифметика наиболее удобна при реализации того, что можно было бы назвать программной арифметикой,— вычислений для управления циклами и индексации, не требующих никаких преобразований данных и, кроме того, столь часто используемых, что применение быстрой арифметики существенно способствует общему быстродействию ЭВМ. При выполнении обработки данных, в которой время выполнения арифметических операций незначительно по сравнению со временем выполнения всей работы, и в частности по сравнению со временем выполнения двоично-десятичных преобразований, более предпочтительной оказывается десятичная арифметика.

Таблица 16.1 Сравнение двоичной и десятичной арифметик

Десятичные константы

Ассемблер при определении констант воспринимает символ Р как признак упакованных десятичных чисел. Например, по команде

THIRTEEN DC Р'13'

ассемблером будет заведена десятичная константа 13, она будет записана в память по адресу THIRTEEN. Итак, в ячейку THIRTEEN будет помещено значение

01ЗС

При отсутствии указания длины ассемблером отводится минимально необходимое место для хранения определенного числа. Иногда, как и в предыдущем примере, константа слева дополняется незначащим нулем, чтобы занимаемое ею поле имело длину, равную целому чисел байтов. Результат всегда является выровненным по правой границе. Длина, как, например, в

ONE DC PL4`T`

означает количество отводимых для хранения константы байтов, а не количество цифр в ней. Выполнение приведенной выше команды дало бы

ONE: 0000001С

Если указываемого количества байтов не хватает для записи числа, соответствующее количество старших разрядов теряется. Результатом выполнения предложения

TOOMUCH DC PL2' —583679'

является

TOOMUCH: 679D

В командах десятичной арифметики допускается указание литералов. Например, по команде

АР COUNT (5), = Р'Г

к 5-байтовому десятичному числу, хранящемуся в памяти под адресу COUNT, будет добавлена 1.